- 等式の自動求解・定理証明
コンピュータに数学の問題を解かせるための基礎研究 - 宣言的プログラミング言語
次世代のプログラミング言語(コンピュータに命令するための人工言語)の設計に関する研究 - 視覚的・対話的プログラミング環境
子どもがコンピュータを操りながら数学的・論理的能力を伸ばすことができる環境の実現をめざした研究
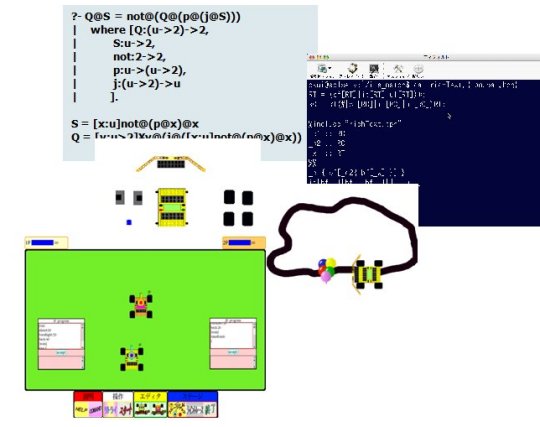
書換え系の合流性(Church-Rosser性)の研究
書換え計算系の合流性を保証する多重危険対とよぶ新たな手法を考案
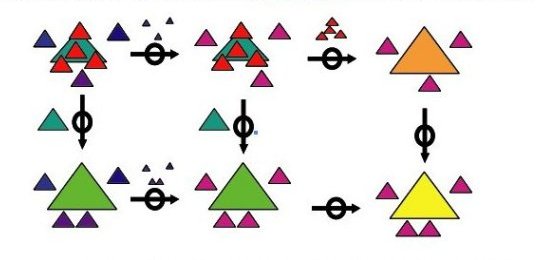
図:多重危険対にもとづく手法により合流性が得られる様子[矢印は項(式)の書換えを、三角は部分項をあらわす]
ナローイングによる等式の求解法とその完全性の研究
遅延ナローイング計算系とよぶ新たな等式求解技法を提案、その求解完全性の証明
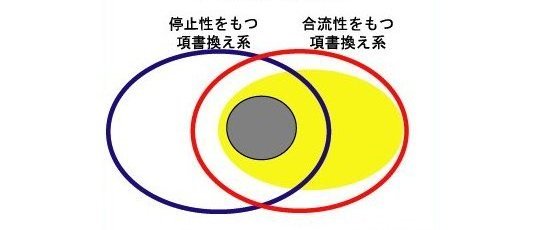
図:遅延ナローイング計算系の適応範囲
灰色:従来の技法の適応範囲、黄色:本手法(停止性を必要としない)
等式にもとづく宣言的プログラミングパラダイムの研究
等式をもちいて宣言的に記述されたプログラムを遅延ナローイングにもとづく処理系が実行
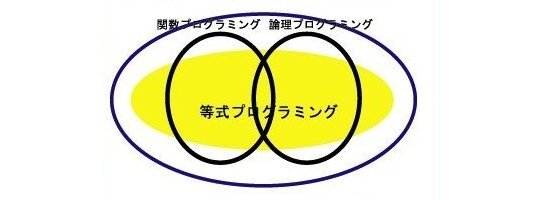
図:等式プログラミングの適応範囲
従来の関数プログラミングと論理プログラミングの特徴をあわせたような記述が可能
現在は高階の記述を許すような一般化を研究中

